$$ \min_{ \boldsymbol{x} \in [0,1]^{Q}} \quad \frac{1}{2}\big|\big| \boldsymbol{y}-\mathbf{H}\boldsymbol{x}\big|\big|{2}^{2}\quad \textrm{ st. } \big|\big|\boldsymbol{x}\big|\big|{0} \leq K, \quad \boldsymbol{1}_{Q}^{\intercal}\boldsymbol{x} =1 $$
Collaborateurs: S.Bourguignon, G.Samain, J.Ninin.
L’imagerie hyperspectrale concerne l’acquisition simultanée d’images dans un grand nombre de longueurs d’onde. Une problématique récurrente de traitement de ces données consiste à résoudre un problème de séparation de sources : en raison d’une faible résolution spatiale des instruments, le spectre de réflectance lumineuse mesuré en une position donnée résulte de la superposition de spectres élémentaires, i.e. un mélange dont il s’agit de retrouver les proportions.
En démélange dit supervisé, le mélange est recherché dans un « dictionnaire » connu de spectres de référence. Une contrainte physique, dite de parcimonie, stipule alors qu’un faible nombre de composants dans le mélange suffit à décrire chaque spectre observé. Mathématiquement, il s’agit d’ajuster un modèle linéaire au sens des moindres carrés, sous la contrainte que le vecteur de coefficients recherchés possède peu de composantes non-nulles, i.e. une faible « norme » $\ell_0$. C’est un problème NP-difficile relevant essentiellement de l’optimisation combinatoire.
Alors que la plupart des travaux dans le domaine considèrent des approches relâchées, privilégiant un faible temps de calcul, nous proposons une méthode de résolution exacte garantissant l’optimalité des solutions obtenues.
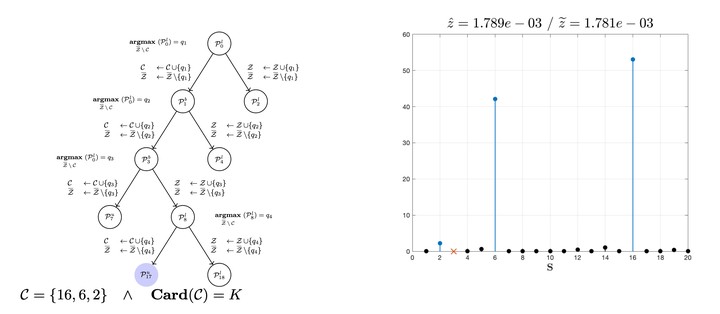
Dans sa thèse de doctorat, Ramzi Ben Mhenni a développé des algorithmes de type branch-and-bound pour l’optimisation parcimonieuse exacte. Nous en proposons ici une version spécifique au problème de démélange. En effet, les coefficients du mélange sont positifs et de somme unité, contraintes qui requièrent une architecture algorithmique spécifique.
Lorsque le mélange est composé d’un nombre restreint de spectres, ce qui est généralement le cas lorsque ces spectres sont « appris » d’un jeu d’observations, nous montrons que cette approche reste peu coûteuse en calcul et fournit des meilleures solutions en comparaison avec les méthodes de la littérature. Lorsque la taille du dictionnaire augmente, e.g. pour un dictionnaire composé d’un grand nombre de spectres mesurés en laboratoire, les solutions obtenues restent de meilleure qualité, au prix d’un temps de calcul bien supérieur.
Un solveur libre, codé en C++, est mis à disposition de la communauté scientifique.
MimosaUnmix_1inst_meth $(pwd) 2 bb_homotopy_fcls eq
L2L0_ASC_ANC_BB_Rhom_fcls
Instance : SA_SNR40_K4_instance30
K = 2 Q = 50 N = 224 ASC form : equality
-----------------------------------------------------------------------
#(it) = 10 #(node) = 19 T = 0.083769 card(L) = 2
xUB* = 1' 34'
UB* = 0.312598 sum(xUB*) = 1
-----------------------------------------------------------------------
[...]
-----------------------------------------------------------------------
#(it) = 100 #(node) = 199 T = 0.319659 card(L) = 1
xUB* = 24 39'
UB* = 0.170461 sum(xUB*) = 1
-----------------------------------------------------------------------
SA_SNR40_K4_instance30 - bb_homotopy_fcls
T = 0.322625 (s)
#(node) = 211 / best(node) = 221
UB* = 0.170461
xUB* :
x(24) = 0.234965
x(39)' = 0.765035
sum(xUB*) = 1